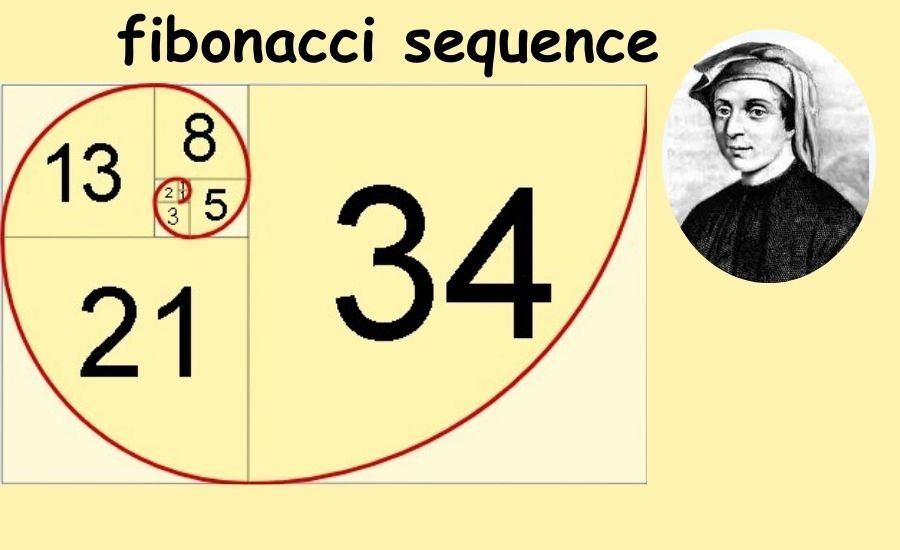
The Fibonacci sequence is a fascinating pattern of numbers that shows up in many places, from the petals on flowers to the spirals in seashells. This sequence starts with 0 and 1, and each new number is the sum of the two before it. So, it goes 0, 1, 1, 2, 3, 5, 8, and so on, with numbers growing bigger as the sequence continues. It isn’t just fun to learn—it also connects us to the beauty and patterns found in nature.
You might be surprised to learn how often it appears around us. Many plants grow in patterns that follow this number sequence. The golden ratio, closely related to the Fibonacci sequence, is often seen as pleasing to the eye and has been used in art and architecture for centuries. Understanding this sequence can give us a new way of looking at the world and help us see the hidden order behind what may seem random.
What is the Fibonacci Sequence?
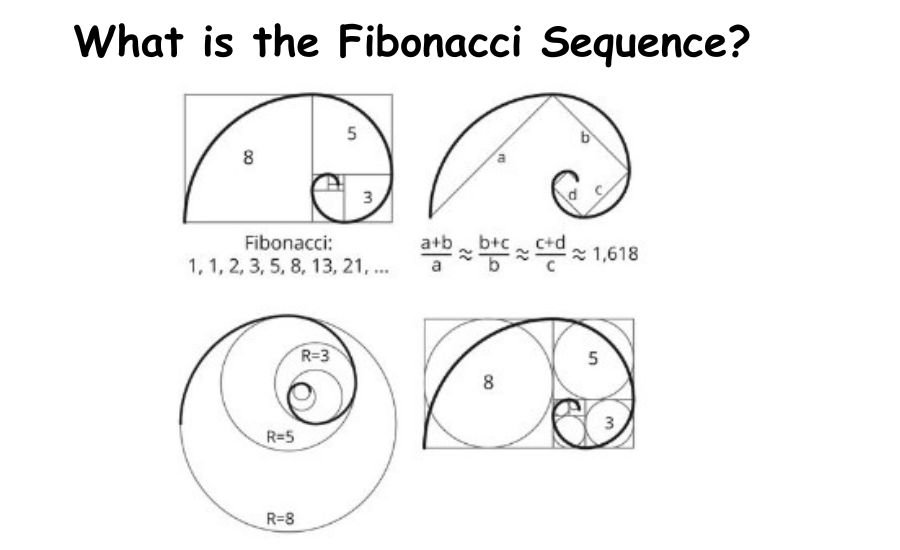
The Fibonacci sequence is a set of numbers that starts with 0 and 1, and each following number is the sum of the two before it. It looks like this: 0, 1, 1, 2, 3, 5, 8, 13, and so on. It’s a simple yet powerful pattern that can be found in many places in nature. For example, the third number in the sequence is 1, which is the sum of 0 and 1.
The fourth number is 2, which is the sum of 1 and 1. This continues endlessly, growing larger with each new number. It’s an important concept in mathematics that has many uses in different fields. In nature, we can find this pattern in how plants grow, animals breed, and even how galaxies spin. The Fibonacci sequence shows up in places we might never expect, making it a fascinating topic to study.
How Does the Fibonacci Sequence Work in Nature?
The Fibonacci sequence is not just a mathematical idea; it also appears in the natural world. For example, sunflower seeds are arranged in a spiral pattern that follows it. If you look closely at a sunflower, you’ll see that the seeds grow in spirals, with each spiral being related to the Fibonacci numbers. Another example is the growth of trees and plants.
Many plants grow leaves in patterns that follow it to maximize sunlight and space. This makes the Fibonacci sequence a hidden blueprint in nature. In some animals, such as honeybees, the number of males to females also reflects the Fibonacci sequence. This pattern shows how deeply embedded this number series is in the world around us.
The Function of Golden Ratio in The Fibonacci Sequence
The Fibonacci sequence is closely linked to the golden ratio, which is approximately 1.618. As you move further along in it, the ratio between each number gets closer and closer to the golden ratio. This ratio is often seen as aesthetically pleasing and is used in art, architecture, and design.
The golden ratio creates harmony and balance, which is why it is found in famous works of art like the Parthenon and even in nature’s designs, such as the spiral of seashells. By studying the Fibonacci sequence and its connection to the golden ratio, we gain a better understanding of how patterns influence the world around us.
The History of the Fibonacci Sequence
The Fibonacci sequence is named after Leonardo Fibonacci, an Italian mathematician who introduced this number pattern to the Western world in his book Liber Abaci, published in 1202. In this book, Fibonacci explored the mathematical patterns behind everyday problems, including a now-famous scenario involving rabbit populations, which demonstrated how numbers in the sequence grow. However, Fibonacci wasn’t the first to discover this sequence.
Ancient Sanskrit texts from India reference similar sequences, indicating that people had noticed these patterns long before Fibonacci’s time. In these early texts, the sequence was likely used for poetic rhythms and calculations, showing its universal appeal across different cultures. Today, the Fibonacci sequence is celebrated not only as a mathematical curiosity but also as a foundation for exploring patterns in nature, art, and science. It has become a universal symbol of growth and structure, connecting diverse fields and fascinating minds worldwide.
Fibonacci Sequence in Art and Architecture

The Fibonacci sequence and the golden ratio are used in art and architecture to create visually appealing designs. The Parthenon in Greece and Leonardo da Vinci’s “Vitruvian Man” both incorporate the Fibonacci sequence to achieve balance and harmony. Artists and architects have used this sequence for centuries to design buildings, paintings, and sculptures that are aesthetically pleasing to the eye.
The ratio provides a natural sense of order and proportion, making it easier for humans to find certain designs beautiful. In modern times, graphic designers and architects still apply it to create layouts and structures that feel naturally balanced. The Fibonacci sequence is deeply tied to how nature organizes and optimizes space, growth, and energy, revealing the hidden harmony in natural growth patterns.
How to Use the Fibonacci Sequence in Finance
The Fibonacci sequence isn’t just for mathematicians or artists. It is also used in finance, particularly in technical analysis. Traders use Fibonacci retracement levels to predict potential price movements in stocks, forex, and other markets. By drawing lines at Fibonacci levels like 23.6%, 38.2%, and 61.8% on a price chart, traders can identify where a market might reverse direction.
These levels are seen as key areas of support and resistance, making the Fibonacci sequence a valuable tool for investors. Though the sequence doesn’t guarantee success, many traders believe that it can help them predict price movements with greater accuracy. This sequence, though ancient, continues to play a modern role in computer science by offering insights into algorithmic optimization and data processing techniques.
Fibonacci Spiral: What is It?
The Fibonacci spiral is a pattern that can be drawn using squares whose sides follow the Fibonacci numbers. The spiral gets bigger as it moves outward, and it appears in many natural objects such as shells, hurricanes, and galaxies. The Fibonacci spiral is related to the golden ratio, as each quarter turn of the spiral follows the proportions of the golden ratio.
This spiral can be found in flowers, plants, and even in the way some animals grow. Understanding the Fibonacci spiral helps us appreciate the beauty and efficiency of nature’s designs, which often follow mathematical principles like the Fibonacci sequence.
Fibonacci Sequence in Animal Kingdom
The Fibonacci sequence also shows up in the animal kingdom. For instance, honeybees follow Fibonacci numbers in their mating habits. A female bee has one parent, while male bees have two. This results in a population pattern based on Fibonacci numbers. Some animals’ physical features also follow Fibonacci patterns.
The horns of certain animals, such as rams, curl in spirals that align with the Fibonacci sequence. Even the arrangement of scales on a pinecone or the structure of a nautilus shell reveals the influence of the Fibonacci sequence. This connection shows that it is not just a human invention, but a natural phenomenon.
Fibonacci Numbers in Plant Growth
Fibonacci numbers can be observed in the way plants grow. For example, a branch of a tree will grow from a point that follows a Fibonacci pattern. Leaves and branches are often arranged at specific angles to optimize sunlight exposure. The spiral pattern of sunflower seeds and pinecones is another clear example of Fibonacci numbers in nature.
This arrangement allows the seeds to grow efficiently and makes the most use of the available space. Even flowers often follow this pattern, with petals that increase in Fibonacci sequence order. From daisies to lilies, the arrangement helps each flower bloom fully, ensuring they thrive in their environment.
The Fibonacci Sequence and Computer Programming

In computer programming, the Fibonacci sequence serves as a classic example for learning recursion, a process where a function calls itself to break down complex tasks into simpler ones. A recursive function can be used to calculate Fibonacci numbers, making it an ideal learning tool for new programmers to understand the concept of recursion. Beyond teaching, Fibonacci numbers have practical uses in programming.
For example, Fibonacci-based algorithms can help with searching and sorting tasks. The Fibonacci search algorithm, for instance, leverages the sequence’s unique properties to efficiently locate elements in a sorted list, making it faster and less memory-intensive for certain types of data. By studying the Fibonacci sequence, programmers can enhance their problem-solving skills and write more efficient code.
Essential Information: Vidqu-face-swap-the-ultimate-fun-and-creative-tool
Fibonacci Sequence in Music
The Fibonacci sequence has even made its way into the world of music, where some composers use it to structure their pieces. For example, musicians may use Fibonacci numbers to determine the length of musical phrases, creating a natural flow and balance that mirrors patterns in nature. One famous example is the band Tool, who incorporated the Fibonacci sequence into their song “Lateralus.”
In this song, the syllables of the lyrics follow the Fibonacci pattern, adding a unique rhythmic quality that feels organic and captivating to listeners. By using Fibonacci numbers, artists can design music with patterns that appeal to our senses, combining the precision of mathematics with the beauty of art. This approach shows how it continues to inspire creativity across various forms of expression, giving music an added layer of depth and harmony.
The Fibonacci Sequence and Human Anatomy
The Fibonacci sequence can also be found in the proportions of the human body. For instance, the ratio of the length of a person’s forearm to their hand often approximates the golden ratio. Other examples can be seen in the spiral of the human ear and the way the bones in our fingers grow. These naturally occurring patterns remind us that the Fibonacci sequence is deeply embedded in our biology.
By studying these patterns, scientists can learn more about the ways in which our bodies are designed. It’s fascinating to see how this sequence even influences how we move, with proportions in muscle length and body structure that help us stay balanced and coordinated. The presence of Fibonacci patterns in human anatomy underscores a natural harmony, linking us to the same mathematical rules that shape the wider natural world.
Fibonacci Sequence and the Universe
The Fibonacci sequence even appears in the structure of galaxies and the spirals of stars. The Milky Way, for example, has a spiral shape that follows the Fibonacci pattern. The idea of spirals is not just limited to earthly objects; it’s seen throughout the universe in the formation of galaxies, planetary systems, and nebulae. This makes the Fibonacci sequence a universal principle that connects the smallest and largest parts of our cosmos.
In this way, it is not just a mathematical curiosity but a key element in understanding the natural world. By observing these patterns, astronomers gain insight into the forces shaping our universe, from the swirl of galaxies to the paths of comets and stars. It’s incredible to think that a simple sequence of numbers might help explain the grand design of the cosmos itself.
How to Spot Fibonacci Sequence in Everyday Life

Fibonacci patterns are everywhere, even in everyday objects. Whether it’s the spiral shape of a seashell, the petals of a flower, or the arrangement of leaves on a tree, the Fibonacci sequence is at work. Learning to recognize these patterns can help us appreciate the beauty of nature and understand how the world is designed.
Even in architecture and technology, Fibonacci numbers are used to create balanced and pleasing designs. By keeping an eye out for Fibonacci patterns, we can start to see the world through a new, more mathematical lens. From pinecones to pineapples, these patterns reveal the hidden order around us. Noticing them adds wonder to daily life, helping us feel connected to nature’s design and even our place within it.
The Future of the Fibonacci Sequence
The Fibonacci sequence is more than just a mathematical curiosity; it is a tool that has been applied in countless fields and continues to be useful today. From art to technology, the sequence’s influence is widespread. As new discoveries are made and technologies evolve, it will likely continue to play a significant role in understanding patterns in nature, designing new innovations, and improving our daily lives.
Its presence in machine learning, digital design, and even data analysis shows its enduring relevance. With so many applications and endless possibilities, the Fibonacci sequence remains one of the most fascinating and enduring mathematical patterns of all time. Its universal appeal suggests that, even centuries from now, it will still inspire curiosity, creativity, and discovery across various disciplines.
Conclusion
The Fibonacci sequence is a fascinating pattern that shows up in so many surprising places—from nature to art, and even in the universe. This simple series of numbers, where each number is the sum of the two before it, forms a foundation for understanding how things grow and organize in the world around us. It’s incredible to think that something as basic as a number pattern can be found in sunflower seeds, seashells, and even the spirals of galaxies. The it reminds us that math isn’t just about solving problems on paper; it’s a language that nature speaks, a code that helps explain how things work in harmony.
Whether it’s in how plants arrange their leaves for sunlight, how artists design balanced artwork, or how traders try to predict stock movements, it plays a role in creating beauty and balance in everyday life. Learning about this sequence can help us appreciate the connections between math and the natural world, showing us that even simple ideas can have a big impact. As we continue to explore and understand these patterns, we gain a deeper appreciation for the math all around us and how it helps shape our lives. With the Fibonacci sequence, we’re reminded that math is not just a subject, it’s a way of seeing the world.
Read You Have To Know: Fujifilm-x100v
FAQs
What is the Fibonacci sequence?
The Fibonacci series is a sequence of numbers in which each number is the sum of the two earlier than it. It starts with 0 and 1, so the sequence goes 0, 1, 1, 2, 3, 5, 8, and so on.
Who discovered the Fibonacci sequence?
The sequence is named after Leonardo Fibonacci, an Italian mathematician who introduced it to the West in his book Liber Abaci in 1202. However, similar patterns were noted in ancient Indian mathematics.
Why is the Fibonacci sequence important?
It is important because it appears in many natural patterns, like the arrangement of leaves, flowers, and shells. It also helps us understand growth patterns and proportions in nature.
How is it related to the golden ratio?
As it progresses, the ratio between two consecutive numbers approaches the golden ratio (approximately 1.618), which is often associated with beauty and balance in art and nature.
Can the Fibonacci sequence be found in nature?
Yes, the Fibonacci sequence appears in nature in the form of spiral patterns in flowers, shells, and even galaxies. This sequence helps explain efficient growth and arrangement in natural structures.
How is it used in art and design?
Artists and designers use it and the golden ratio to create visually pleasing compositions, as these proportions are naturally harmonious to the human eye.
Is the Fibonacci sequence used in finance?
Yes, in finance, the Fibonacci sequence is used in technical analysis to predict stock trends and price retracements, though it’s only one of many tools analysts use.
How do you calculate numbers in the Fibonacci sequence?
To find a number in it, you add the two numbers before it. For example, after 3 and 5, the next number would be 3 + 5 = 8.
What is a practical use for it?
Aside from its natural appearances, the Fibonacci sequence is used in computer algorithms, financial trading, and creating efficient layouts in architecture and web design.
Can the Fibonacci sequence go on forever?
Yes, theoretically, it is infinite. By continuing to add the last two numbers, you can always generate the next number in the sequence endlessly.